Why is Quantum Computing so Exciting and How Can It Be So Powerful?

[Editorial Note: This was the very first Quantum Leap blog post, originally posted October 7, 2021 and modestly revised to keep it current.]

If you are reading this blog, you are likely already familiar with some of the essential features of Quantum Computing like superposition and entanglement.  Even if you are not, I will cover some of those details in future posts.  For now, I wanted to begin without any physics or linear algebra and instead give you some layman observations about Quantum Computing to establish a fundamental understanding of the potential that quantum computing holds.  For those of you that are more familiar with some of these underlying principles, please allow me to take some liberty as I describe them.  I am more interested at this point with conveying a general sense for why quantum computing has so much more power than classical computing (at least for certain problems), so will generalize some things in ways that may not be explicitly or literally correct.

If you are early in your quantum journey, you are likely to find it to be a lot like buying a 1,000 piece, two-sided puzzle without edges and dumping the pieces on the table.

There are a jumble of new phrases and concepts, but for now, let’s dispense with the peculiarities of why Schrodinger’s cat can be both alive and dead, why Heisenberg talks about uncertainty and why Einstein famously said that “God does not play dice with the universe.”  And, with powerful deference to Richard Feynman, the modern godfather of quantum theory, you don’t need to understand the specifics of quantum mechanics to grasp the enormous potential of Quantum Computing.

I think we all appreciate the awesome power of the microchip and the advances in technology (and creature comforts) it has provided without understanding the actual engineering of the silicon chips or transistors or integrated circuits that underlie current computers. 

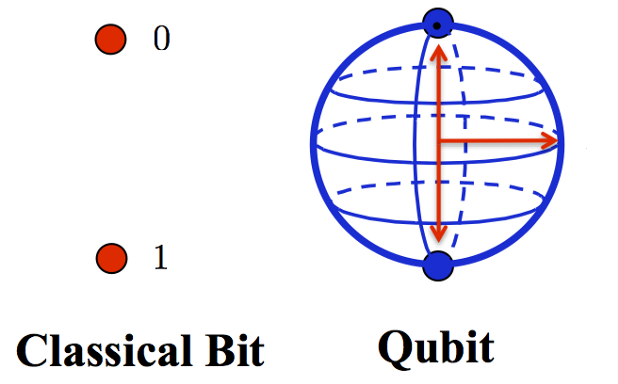
So, if you’ll indulge me for a bit here, let me try and convey the potential of the powerful new computing methodology of quantum, without reference to superposition or Josephson Junctions or coherence or error correction (I’ll cover those in subsequent posts).  Let’s start with some fundamental features of classical computer “bits” versus quantum computer “qubits”.  As you may know, classical computers use “bits” to establish a binary yes/no or on/off state which is then interpreted in algorithms to perform calculations.  These bits are combined into bytes to represent letters and numbers, among other things.  Let’s picture a bit as a one-dimensional creature (this takes some liberties, since a one-dimensional object is a line, but bear with me here).  The first fundamental difference between classical computing and quantum computing is that the qubit is a three-dimensional structure.  The following graphic showcases this difference^[1]:

As the graphic shows, the Classical Bit is always and only in one of two states.  It is either “0” or “1”.  For the Qubit, if “up” is considered as “0” and “down” is considered “1”, until it is measured it can be pointing in any direction among the 360-degree sphere, so think of that as holding lots of additional information besides just up or down. Or to think about it another way, a Qubit has more dimensions than a Bit and so it can process more information per step and therefore can speed up the processing.

So, the first major difference between classical and quantum computing lies in having three dimensions for the underlying data bits vs just one dimension for classical computers.   This by itself suggests enormous added potential of quantum computing.

Next, let’s dig in a bit further to how these bits/qubits are processed. Computers use the information contained in the bits to process according to its program or computer code. So, an original input is entered into a processor, and it spits out an output based on some rules contained in the processer. Each step or operation is generally referred to as a “gate” or basic computing step. It turns out there are three gates from which ALL current classical computing processes derive their output. While not essential to this discussion, these three gates are “AND”, “OR” and “NOT”. Stacking and using combinations of these rules, or gates, can perform every Boolean logic operation that exists in classical computers ^[2]. Generally, you should take this to mean that ALL classical computing can currently be done with only 3 operators, which conversely suggests that the universe of possible computational abilities is somewhat limited to only three rules. Consider it like a chess pawn which can only move to one of three squares when being played. For single quantum “gates”, again without getting into the details, know that there are at least 6 primary gates (not that it is needed for this train of thought, but they include the three Pauli X, Y and Z Gates, the Hadamard Gate, the SWAP Gate and the CNOT or Controlled Not Gate). There are others, and Entanglement allows gates to be conjoined, if you will, but let’s stick with 6 for this discussion. So, coming back to the chess analogy, this is like the movement potential of the queen and if we consider a contest between a classical computer, which only has pawns as its pieces, versus a quantum computer which has all queens, it is clear which would win the chess match.

Hence, the second major difference between classical and quantum computing is a result of the essential gates that can be utilized to perform operations.  Classical uses three and quantum uses six. Think about this as enabling a Qubit to do more per process, which translates into being able to process things faster.

The final major difference between classical computers and quantum computers is rooted in the computing logic “efficiency”. We are all familiar with the physical noise that nearly all current computer emits, which is the sound of the fan. We also know how hot a computer can get with usage. This is because classical computing processing causes a “loss” of information whenever a calculation is performed, which is lost in the form of heat. This is because classical computer gates are one-directional. Because energy is expended by the gate and information is lost, if you perform a calculation on a classical gate, you cannot run the output in reverse through the gate to get the original input. However, quantum gates are bi-directional, meaning that any output can be reversed through the gate with the original input revealed.

The final major difference between classical and quantum computing is that classical computing operators are one-directional and not reversible, while quantum operators are bi-directional. This bidirectionality suggests more processing information per operation, which also translates into being able to operate faster.

In summary we have the following:

Think about these differences as enabling a Quantum Computer to do more per step, which is another way of saying it can process things faster than a classical computer. As it turns out, this speed advantage is phenomenal, which is why there is such enormous potential for Quantum Computers. In future posts, I will cover how this phenomenal speed advantage manifests and why it will allow us to solve problems currently unsolvable by the most powerful supercomputers.

I hope this helps convey the potential of Quantum Computers over classical computers, without any details around superposition or entanglement or the underlying non-intuitive features of quantum mechanics. Naturally a greater knowledge of those other concepts are fundamental to the actual inner-workings of a Quantum Computer and I will get into some of that in future posts.

---

References:

[1] Image from “The Need, Promise, and reality of Quantum Computing” by Jason Roell, published on Medium 2/1/18.

[2] Technically, either the NOR (Not Or) or NAND (Not And) gates are considered "universal" meaning either can be used to reproduce the functions of the other gates, so technically, current digital computing logic can be done with ONE gate, but the analysis herein, assuming the three core gates, is still quite solid vis-a-vis the greater number of core gates applicable to quantum gates. For further details, consider Logic gate - Wikipedia

Russ Fein is a venture investor with deep interests in Quantum Computing (QC).  For more of his thoughts about QC please visit subscribe to his Quantum Leap Substack. 

For more information about his firm, please visit Corporate Fuel.  Russ can be reached at russ@quantumleap.blog.