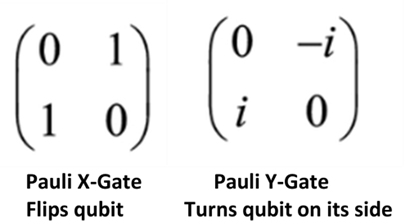Ways to Appreciate Quantum Computing Power

Here are some intuitive descriptions of how Quantum Computers can be so powerful

This post is for readers interested in a bit more detail on how the principles of quantum mechanics can be leveraged for Quantum Computing. It starts with some descriptions that exclude mathematics, then layers on some added explanations with only modest math and physics. While a reader does not need to master any of these concepts to appreciate the business (and investment) potential of Quantum Computers, it is hoped that this post will provide added insights on the power of quantum.

Phase I – No Math Required

Key Principle: Quantum mechanics operate with different rules.

Classical physics (sometimes referred to as Newtonian Physics) generally describes what we can see in the world around us. Newton’s three laws summarize these physics as:

1. Force = mass x acceleration;

2. For every action there is an equal and opposite reaction; and

3. A body at rest tends to stay at rest and a body in motion tends to stay in motion.

You don’t need to understand the mathematics behind these principles to hit a golf ball towards a hole, or to strike a cue ball to hit another billiard ball into a pocket. Yet there are precise mathematics that can explain (and predict) these actions. Quantum mechanics have very different rules and very different mathematics to explain and predict quantum behavior, and you can get a feeling for the power without understanding the underlying physics. So, without any of the math, the following table highlights some essential principles of quantum mechanics:

Key Takeaway: the physics underlying quantum mechanics adds many interesting new actions to leverage, providing increased power and capabilities.

Phase II – High School Senior Level Math (Logic)

Key Principle: The “compute space” for Quantum Computing is vastly larger than that of classical computing.

As some readers may know, classical computers such as the PC or Mac you use for email, web surfing or creating spreadsheets, use underlying memory or processing units that are binary. These classical computers are driven by integrated circuits which manipulate “bits” which are switches that are either ‘on’ or ‘off’ and translate into either ‘1’ or ‘0’ (i.e., are binary, or take one of two values and operate in only 1-dimension).

A classical computer, at its most fundamental level, takes some “input” or data, then applies certain rules or formulas to such input thereby changing the data, and then reads the “output.” These rules or formulas (also referred to as programs) operate in only one direction (the heat that your computer generates is the loss of information that these programs experience as they are run). As noted above, the data is stored as binary bits which are manipulated by programs that apply Boolean logic, and 100% of all classical computing is driven by Boolean logic that can be implemented by just three different rules or gates: ‘AND’, ‘NOT’ and ‘OR’. So, at its rudimentary level, classical computers take binary code, implement some combination of only 3 rules, and then output and read the results. Today’s classical computers have billions of circuits and can apply these rules incredibly fast (gaming PCs operate at ~4GHz meaning they can manipulate 4 billion bits per second). Clever programmers have found increasingly efficient and profound ways to implement programs despite having only two inputs (1 or 0) and only three logic gates.

A quantum computer, leveraging quantum mechanics, has a different set of inputs, rules, and constraints. Instead of binary bits, quantum computers use “qubits”, which can be placed in a superposition meaning they can be ‘1’ or ‘0’ or some combination of both (a weighted average of the two states). In addition, qubits are 3-dimensional objects so the qubit can be oriented in any direction among those three dimensions. These 3-dimensional inputs can be manipulated by more than just the 3 rules that limit classical computing. There are at least 6 primary rules or gates that can be applied (X, Y and Z Gates, which rotate the qubit along those dimensional axes, and the Hadamard, Phase and T- Gates which essentially rotate the qubit in different ways). Plus, since qubits can be entangled, there are various multi-qubit gates as well (the “CNOT” also known as the “Controlled Not” gate being a primary example).

So, for Quantum Computing, the fundamental unit is the qubit, and the qubit has significantly more ways it can be input and manipulated versus its classical bit counterpart, summarized in the following table:

A useful analogy is that of chess pieces. Classical computers have, essentially, only Pawns to use whereas quantum computers have Queens. Any readers familiar with chess can imagine who would win if one player only had Pawns to use while the opponent had a side filled with Queens.

Key Takeaway: Qubits operate in more dimensions with more operators which combines to provide a profoundly larger “compute” space. Imagine what those clever programmers will be able to achieve with this vastly larger space.

Phase III – Some College Level Math (Linear Algebra)

Key Principle: Quantum Computers can access more dimensions, which provides an entirely new computing paradigm.

Using very elementary linear algebra, we can depict quantum computing gates with matrix notation, as highlighted in the graphic below. On the left is the Pauli ‘X-Gate’ which is analogous to the ‘NOT’ gate in classical computing. If you apply a NOT gate in classical computing, it switches a ‘1’ to a ‘0’ or a ‘0’ to a ‘1’. In Quantum Computing the X-Gate essentially flips the qubit on its head, also switching a |1〉to a |0〉or a |0〉to a |1> (now using the bra-ket notation more common in quantum computing and linear algebra). This is straight forward only requiring the most basic familiarity with matrix multiplication to prove it. However, the “Y-Gate” is quite different. The Y-Gate essentially turns the qubit on its side, and its matrix representation is suddenly quite foreign. The matrix representation of these two gates is shown below:

You will note for the Y-Gate the introduction of “i” (and “-i") which is the symbol for the unfortunately named “Imaginary” number. “i”’ is mathematically defined as the solution to X²+ 1 = 0. Although there is no “real” number that can solve this equation, it can still be used for certain mathematical functions. It would be more fitting to call these “complex” numbers instead of imaginary. Mathematicians would likely describe “i” as “lateral” or “perpendicular” to the plane where the “Real” numbers lay. Evoking this concept of “Real” versus “Imaginary” suggests the imaginary numbers are surreal or mystical but what it shows is that the information is quite different when orienting along the X-Axis versus orienting perpendicularly on the Y-Axis. The same qubit holds different (i.e., more) information depending which way it is oriented.

Key takeaway: The same quantum “thing”, oriented in one direction, contains different information if you orient it in a perpendicular manner. Said another way, Quantum Computers allow us to expand the number of dimensions being utilized, analyzed, and manipulated. More dimensions mean more power…profoundly more.

Putting It All Together

It is profound to think of the power in today’s classical computers, including the recent surge in Artificial Intelligence. As Moore’s Law has evolved over the 50 years since it was first postulated by Gordon Moore (essentially predicting that the density of computer chips would double every two years), computers have become increasingly powerful and computer programmers have creating some amazing programs, despite only have binary bits and 3 logic gates.

Today, we have very early generation quantum computers, although they are still not powerful enough to run sophisticated quantum algorithms. So, the budding quantum programmers don’t yet have the ability to leverage the full power of quantum and its extra dimensions and gates. In fact, not many practical quantum programs exist yet (with the notable exceptions of Shor’s Algorithm and Grover’s Search Algorithm) so it’s hard to appreciate what this extra power will actually be able to do. Hopefully this post has given you some sense of what may be possible, and I look forward to seeing the amazing things that clever programmers will do with this new power.